Homogenous Coordinates
Homogenous coordinates utilize a mathematical trick to embed
three-dimensional coordinates and transformations into a
four-dimensional matrix format. As a result, inversions or
combinations of linear transformations are simplified to inversion or
multiplication of the corresponding matrices. Homogenous coordinates
also make it possible to define perspective transformations.
4x1 Homogenous Coordinate Vectors
Instead of representing each point (x,y,z) in three-dimensional
space with a single three-dimensional vector:
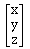
homogenous coordinates allow each point (x,y,z) to be represented by
any of an infinite number of four dimensional vectors:

The three-dimensional vector corresponding to any four-dimensional
vector can be computed by dividing the first three elements by the
fourth, and a four-dimensional vector corresponding to any
three-dimensional vector can be created by simply adding a fourth
element and setting it equal to one.
Many textbooks define homogenous coordinates in such a way that
points are represented by 1x4 vectors:
[T*x T*y T*z T]
instead of 4x1 vectors. This definition is not used in the AIR
package and results in different 4x4 homogenous coordinate
transformation matrices than those described below.
4x4 Homogenous Coordinate Transformation
Matrices
Homogenous coordinate transformation matrices operate on
four-dimensional homogenous coordinate vector
representations of traditional three-dimensional coordinate
locations. Any three-dimensional linear transformation (rotation,
translation, skew, perspective distortion) can be represented by a
4x4 homogenous coordinate transformation matrix. In fact, because of
the redundant representation of three space in a homogenous
coordinate system, an infinite number of different 4x4 homogenous
coordinate transformation matrices are available to perform any given
linear transformation. This redundancy can be eliminated to provide a
unique representation by dividing all elements of a 4x4 homogenous
transformation matrix by the last element (which will become equal to
one). This means that a 4x4 homogenous transformation matrix can
incorporate as many as 15 independent parameters. The generic format
representation of a homogenous transformation equation for mapping
the three dimensional coordinate (x,y,z) to the three-dimensional
coordinate (x',y',z') is:

If any two matrices or vectors of this equation are known, the third
matrix (or vector) can be computed and then the redundant T element
in the solution can be eliminated by dividing all elements of the
matrix by the last element.
Various transformation models can be used
to constrain the form of the matrix to tranformations with fewer
degrees of freedom.
In many textbooks, you will find homogenous tranformation matrices
defined such that 1x4 homogenous coordinate vectors are placed to the
left of the 4x4 homogenous coordinate transformation matrix and
multiplied. This format is not supported in the AIR package and the
difference accounts for the fact that translations are represented in
the fourth column and perspective distortions in the fourth row of
AIR homologous transformation matrices rather than vice versa.
Translations
Translations can be represented by the 4x4 homogenous coordinate
transformation matrix:

Rotations
A series of rotations (in the order [roll matrix]*[pitch
matrix]*[yaw matrix]) can be represented by the 4x4 homogenous
coordinate transformation matrix:

Rescaling
Rescaling along the major axes can be represented by the 4x4
homogenous coordinate transformation matrix:

Perspective
Perspective distortion is achieved by applying the 4x4 homogenous
coordinate transformation matrix:

 Modified: December 10, 2001
Modified: December 10, 2001
© 1995-2001 Roger P. Woods,
M.D.(rwoods@ucla.edu)






 Modified: December 10, 2001
Modified: December 10, 2001